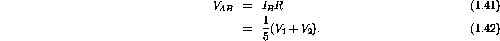This method is also referred to as the mesh loop method. The independent current variables are taken to be the circulating current in each of the interior loops.
Depending on the problem, it may ultimately be necessary to algebraically sum two loop currents in order to obtain the needed interior branch current for the final answer.
Lets consider the example of the Wheatstone bridge circuit shown in
figure 1.6.
We wish to calculate the currents around the loops.
The three currents are identified as: 
the clockwise current
around the large interior loop which includes the EMF, 
the
clockwise current around the top equilateral triangle, and 
the
clockwise current around the bottom equilateral triangle.
The voltage loop expressions for the three current loops are
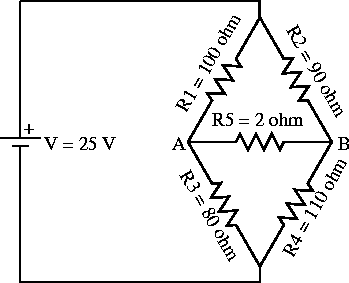
Figure 1.6:
Loop method for the Wheatstone bridge circuit.
Collecting terms containing the same current gives
If the values for the parameters shown in the diagram are used, the current values can be found by solving the set of simultaneous equations to give
Moreover, if we number the individual currents through each resistor
using the same scheme as we have for each component (current through
is 
, 
has 
, etc.) and identify 
as the
current out of the battery, then
These are the same currents that would be found using only Kirchoff's equations; however, here we had to handle only three simultaneous equations instead of six.
Example: Use the loop current method to determine the voltage developed across the terminals AB in the circuit shown in figure 1.7.
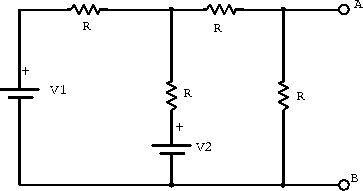
Figure 1.7: Example circuit for analysis using the loop current method.
Consider the clockwise current loop
through the two resistors and the two potentials. Similarly consider the clockwise current
around the other internal loop consisting of the three resistors and
. Kirchoff's law gives
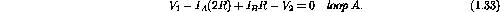
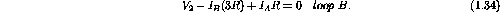
Solving the above two equations for the unknown loop currents
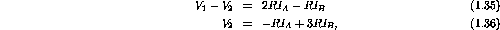
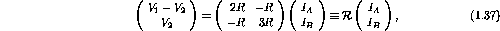
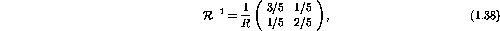
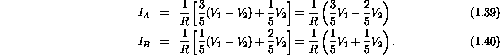
The voltage across AB is given simply by
