

by Terry Newton
Introduction
Described here is a minimalistic robotic platform and a program that I wrote for it. Influencing both the mechanics and the software were ideas from the field of BEAM robotics, a hobby/science that specialises minimalism as an art form and to demonstrate lessons from nature. BEAM comes from the works and ideas of Mark Tilden, combined with the crazy stuff that happens when a bunch of eager robotists not necessarily with electronics experience tinker with concepts more advanced than they realise. One seemingly simple but popular BEAM element is the bicore, the two-neuron form of Mark Tilden's nervous network. Only recently have studies been done on two coupled bicores, and that resists definition. I'm not that versed in higher math, and the why of it interests me much less than exploring what can it do. The program I shall describe simulates the equivalent of five coupled bicores, next to impossible to mathematically describe. Since I cannot pretend to know how such a network should be connected, the software connects itself by simple random selection. To allow adaptation to proceed without barriors, the last bicore is used to drive the motors through differentiators with motor reverse signals coming from opposing feelers, an arrangement similar to Mark Tilden's "Beam Ant" design. Amusing and useful things happen when the connections between the bicores are allowed to reconnect themselves. I hesitate to call it evolution or genetics, as the population size is one (unless the slots I'll get to later count as "members") and only environmental pressure from excessive feeler contact drive the randomising process. Because of the inherent richness of the modes of expression exibited by coupled bicores, self-wiring is particularly easy to implement: try anything, there's a good chance of it doing something useful. I also suspect that networks of coupled bicores connected in arbitrary mannors perform a unique class of computations of their own, capturing data in the phase space between oscillations enabling it to be acted upon later. I suspect the same thing happens in living things.
The provided algorithms simulate a form of nervous network, a robotic control structure invented and patented by Mark Tilden. Commercial use is prohibited unless arrangements are made with the patent holder. A certain amount of my own intellectual property is contained within, the hardware and the software that simulates a network of bicores. The software and schematic design is protected by copyright, commercial use is prohibited unless arrangements are made with Terry Newton and Mark Tilden as well if it involves bicores.
The Platform
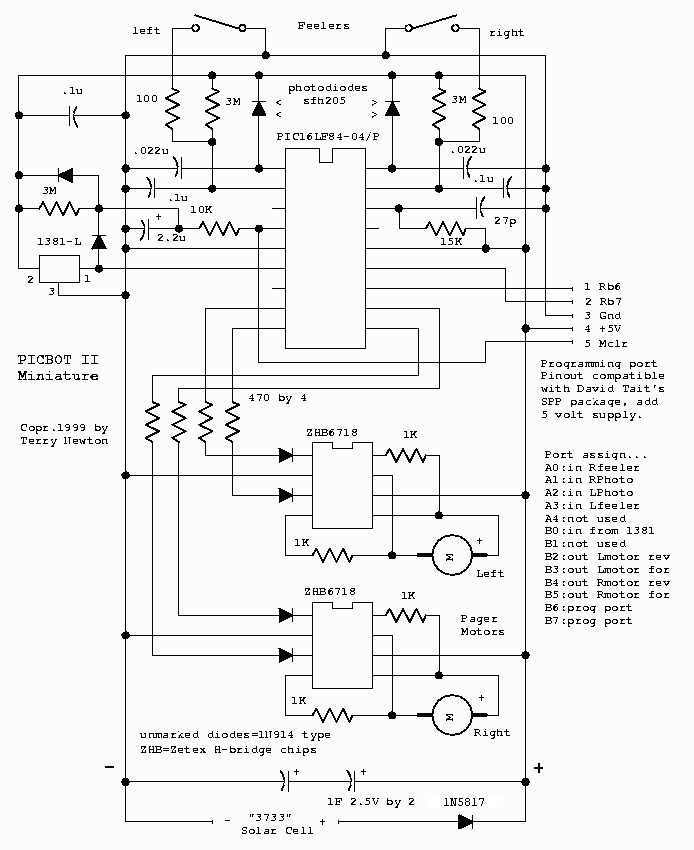
The robot I used for my experiments is a miniature version of my PicBot II design based on a PIC16LF84 processor which features 1K words of program store (14 bit), 68 bytes of ram and 64 bytes of nonvolatile eeprom. Motor signals are amplified by a pair of miniature Zetex H-bridge chips and delivered to a pair of miniature "pager" motors which are angled in the classic BEAM "popper" arrangement. Power is provided by 0.5 farads of capacitive store charged by a 37mm by 33mm solar cell that delivers a maximum of 15ma (usually much less) with an open circuit voltage of approximately 4.8 volts. A voltage trigger chip signals the processor when the charge is greater than 3.2 volts, sufficient for several inches of movement before discharging to the point of sluggishness. After a timed activity phase the software should go to sleep and wait for the trigger to indicate sufficient voltage before moving again. Just in case the programmer overdoes it, and to protect from random processor pin states that occur at low voltages, the H-bridge motor drivers do not respond to low voltage signals. For best results the discharge should not go below about 2.7 volts before putting the processor to sleep.
Pictures of the miniature PicBot II, side view and top view without the solar cell...


Schematic of the miniature PicBot II...
The PIC is programmed in-circuit (has to be since it is soldered in-place) using simple hardware between a PC's printer port and freely available software. The circuit itself is not BEAM, it is what is placed inside the processor that determines what it does and by who's philosophy. The mechanical design however is very BEAM-ish. Was the easiest thing to make.
Controlling an Autonomous Robot with a Processor
One of the big problems with processors is they view the world in discrete steps. Everything is a bit and every number is an integer. This often leads to the programmer trying to specify exactly what each input combination should do:
loop forever... read sensors action = bothforward if lightonleft then action = rightforward if lightonleft then action = leftforward if leftfeeler then action = rightreverse if rightfeeler then action = leftreverse if leftfeeler and rightfeeler then action = bothreverse move robot
This method is useless if the environment is variable and does not yield to such simplistic logic, or the environment is not known well enough for the programmer to predict every combination. Plus it's boring.
It is better if the robot can decide for itself what actions should go with what sensor combinations. This can be directly mapped using memory:
loop forever...
last address = address
address = sensor bits
if feelers are touching too much
or action is a bad move then
randomise memory(last address)
end if
action = memory(address)
move robot
Now the robot is free to pick what it does in response to a given environmental condition, and change its mind if things aren't going well. But it is still direct-mapping. Although many tricks can be applied to improve performance, it cannot corelate the present with the past more than one move except through environmental cues. A more sophisticated structure is needed.
This is where processor meets BEAM. Bicores are basically two-pole oscillators with inputs which affect the time each node takes to change state. Bicores are complementary, anything done to one input has the opposite effect on the other output. If node A is made to be high 70% of the time, node B will be high 30% of the time. This makes things easy since bicore effects show up whether the inputs tend towards high or low or the nodes are active high or low. Differences are compensated for by merely swapping either the inputs or outputs. No attempt was made to make the simulated bicores exactly model real bicores, for one thing real bicores are made with inverters but that's an extra step for a computer, I did what seemed natural at the time. A nice effect one gets from loosely coupling two or more bicores is if the rates are similar they can store information for many cycles in the form of the phase relation between the bicores. When many bicores are coupled with more than one input to each bicore node things get really interesting - the network has, for a given pattern of connections, replicate complex patterns in response to the environment and time. The pattern of interconnections becomes a selector for a wide range of behaviors leading to effects like accidental mapmaking.
But how to take an inherently analog thing like a bicore and run it on an inherently stepped device like a processor? Easy, take tiny steps and don't worry too much about exactly matching reality. Oftentimes the core properties of analog systems show up just fine when 0..1 real is represented as say 0..50 integer. Sometimes the extra nonlinearity helps. Concepts like information coding in phase space and chaotic couplings in recurrent neural networks work fine in discrete steps so long as the steps are not so large they erase the information being encoded. For practical purposes activation levels are restricted from 0 to 127 (usually set much lower) and connection weights vary between 1 and 15, or 0 for no connection.
The following overall structure is used in the self-wiring bicore array program...
loop forever...
if powerpin = high then
check and initialise node states if necessary
loop sensecycle about 15 times
read senses
evaluate last move and score performance,
change network if not performing well
loop microcycle about 60 times
run the network simulation one time slice
compute hard-wired "horse" connections
apply network output to motors
next microcycle
turn off motors
delay briefly for senses to settle
next sensecycle
else
sleep for a few seconds
end if
This general shell is good for simulating many types of real-time networks, not just the nervous variety. For simulating bicores, the initialise step is to ensure that all bicore states begin complementary. Evaluation and network change methods can vary widely, for my experiments these steps are extremely simplistic.
Simulating Evolving Bicores
For evaluation, I hard-coded the "horse" layer so that reversal can only take place in appropriate situations, so that's not a factor. It is wired so that there is no standing still state, so it doesn't have to check for that. Currently it evaluates success or failure at avoiding feeler contact by subtracting from the score if the feelers touch, subtracting more if they touch too much, adding a point if no recent feeler contact and adding several points for feeler touches followed by no touches. This evolves networks that do whatever they can to avoid feeler contact. To "program" other behaviors, other or additional scoring factors can be applied, light level to evolve light-seeking networks for example.
The evolution algorithm is equally simplistic. For diversity, three slots are defined in eeprom, when called upon to save or restore a network it randomly selects one of the three slots. When a network's score reaches a maximum value, it is saved to eeprom. When score drops to 0, a previously saved network is loaded into operating ram. If the network still continues to score poorly, all connections are randomised. For incremental changes a running changeat value is maintained. When score dips below the changeat value, a connection input source or weight value is changed. Bits that cause the feelers to become disconnected from the reversers are randomly changed 25% of the time, giving the robot the ability to temporarily ignore its feelers and squeeze past obstacles that would otherwise block its path. Also randomly changed is the value for the motor differentiators, altering the intensity of motor drive. Often this value tends toward minimum, since that results in the fewest feeler hits per period, saving higher speeds for problem situations.
The network simulation component is where most of the processing occurs, the evaluation and adaptation parts are simple mainly because of the richness of interconnected bicores combined with an effective horse layer based upon Mark Tilden's Beam Ant design. To simulate a bicore one need not be concerned with resistors, capacitors, thresholds and all that, but only consider what a bicore does: it flips from one state to another with the outputs always complementary, and the time it takes to flip is influenced from a nominal value by any inputs applied to it. To handle input for each bicore node an integrating accumulator is used to translate input from multiple sources into a numeric value. Inputs which are currently "on" add their weight to the accumulator, inputs which are "off" subtract their weight. In an oscillating environment the accumulator will hold approximate position if the input duty cycle is exactly 50% but amplify any difference. This is a deviation from most hard-wired bicore networks that was used mainly for convenience but probably has the effect of making the networks more chaotic. To determine the "off" period of a bicore a counter is used, decremented once for each time slice whenever the node is off. When it reaches 0 the node turns on, the opposing node turns off and the counter is reloaded with a value minus whatever is in the input accumulator, thus all inputs are excitory, decreasing the node's "off" time and increasing the frequency.
The following illustrates one time slice of one bicore...
// accumulate input...
// (not necessarily here but somewhere in the loop)
for each input
if connected input node is on then
add connection weight to accumulator
else
subtract connection weight from accumulator
end if
next input
// compute bicore...
for each bicore node
if counter > 0 then
if node is off then
decrement counter
end if
else
turn node on in the next timeslice
turn opposing node off in the next timeslice
counter = baselevel - accumulator
end if
next node // in full pseudocode this loop unwrapped
// to avoid having to define "opposing node"
Note that input activations are delayed until the opposing node relinquishes control, wasn't intentional just how it came out. This is but one way one can simulate bicore-like activity, the most obvious way at the time I wrote the program. I'm sure the method can be improved. For each time slice the bicore proceedure is applied to all of the elements in the array then all of the node states are changed at once. Nodes which drive a motor set the motor's differentiator counter when they trigger and clear the opposing motor's counter. The differentiator counters decrement (down to 0) each time slice, the motor is activated as long as the counter is above 0.
The Full Algorithm
This puts it all of the components together. Each of four bicores have four evolvable connections, two per node. The fourth bicore drives the motor differentiator counters, which drive the forward direction terminals of the motors. The fifth bicore pair, or photo bicore, has inputs hardwired to the absolute light levels and is not evolvable. The numbering scheme for the bicores is arbitrary. The reverse motor terminals are wired to opposing feelers, but are ignored if the corresponding ignore-feeler bit is set. Input sources range from 0 to 15 to represent always 0, leftfeeler, rightfeeler, lightonleft, lightonright, photobicoreA, photobicoreB, badenv, and eight bicore node outputs.
// constants...
punish1 = 4 // for 1 hit
punish2 = 10 // for multiple hits
reward1 = 3 // for clearing after hit
reward2 = 5 // for remaining clear after hit
photopunish = 3 // for current light < previous
photoreward = 3 // for current light > previous
punishment = 10 // for original score and bigscore
maxscore = 50 // max score and bigscore value
startscore = 30 // start values for score and bigscore
changescore = 25 // change if score below this
sensecycles = 15 // how many sense/move cycles to stay awake
microcycles = 60 // how long each sense/move cycle lasts
mindiffval = 30 // minimum motor speed
maxinput = 50 // maximum level of input accumulators
baselevel = 60 // largest starting countdown for timing
// arrays...
sourceA(4,2) // bicore#, input# \
sourceB(4,2) // \ collectively refered
weightA(4,2) // / to as the "network"
weightB(4,2) // /
inputaccA(4)
inputaccB(4)
countA(5) // fifth unit is photo bicore
countB(5) // inputs hardcoded to light level
stateA(5)
stateB(5)
nextstateA(5) // states are bits, either 0 or 1
nextstateB(5)
sourcestate(16) // maps to input bits and bicore outs
loop forever
if powerpin is high then
if any bits in stateA = stateB then fix
loop sensecycle sensecycles times
read senses (sensor bits available to network)
// evaluate performance...
lastbad2 = lastbad
lastbad = badenv
badenv = leftfeeler or rightfeeler
// original scoring function...
// if badenv then
// score = score - punishment
// else
// score = score + 1
// end if
// new scoring function...
if badenv then
if lastbad or lastbad2 then
subtract punish2 from score // punishment for multiple hits
else
subtract punish1 from score // punishment for single hit
endif
else
if lastbad then
add reward1 to score // reward for 1 clear after hit
else
if lastbad2 then
add reward2 to score // reward for 2 clear after hit
else
inc score // reward for clear environment
end if
end if
end if
// score light performance
if leftlight + rightlight > lastlight then // low precision sum
score = score + photoreward // has to really get
end if // brighter/dimmer
if leftlight + rightlight < lastlight then // or no effect
score = score - photoreward
end if
lastlight = leftlight + rightlight
// normalise score from 0 to maxscore
if score < 0 then score = 0
if score > maxscore then score = maxscore
// clear exception bits if clear environment
if not badenv and not lastbad and not lastbad2 then
clear feeler ignore bits
clear motor reverse bits
end if
// evolve network...
if score = maxscore then
select one of three eeprom slots
copy network to selected slot
bigscore = bigscore + 1
if bigscore > maxscore then bigscore = maxscore
score = startscore
else
if score = 0 then
score = startscore
changeat = changescore
if bigscore > 0 then
bigscore = bigscore - punishment
select one of three eeprom slots
copy selected slot to network
else
completely randomise network
bigscore = startscore
endif
else
if score < changeat then
select random connection number (1 of 16)
if random bit is high then
selected input source = random nibble
else
selected weight = random nibble // could be incremental
end if // but didn't bother
if two random bits = 11 then
randomly change L/R feeler ignore bits
end if
if two random bits = 11 then
randomly change DiffNum // 0-7 to represent
end if // differentiator value
if two random bits = 11 then
randomly change L/R motor reverse bits
end if
end if
end if
end if
// set up microloop
diffvalue = mindifval + DiffNum * 4
loop microcycle microcycles times
// run bicores
nextstate(all) = state(all)
for bicore = 1 to 5
if countA(bicore) > 0 then
if stateA(bicore) = off then
countA(bicore) = countA(bicore) - 1
end if
else
nextstateA(bicore) = 1
nextstateB(bicore) = 0
countA(bicore) = baselevel - inputaccA(bicore)
if bicore = 4 then // if motor bicore
motordiffL = diffvalue
motordiffR = 0
end if
end if
if countB(bicore) > 0 then
if stateB(bicore) = off then
countB(bicore) = countB(bicore) - 1
end if
else
nextstateB(bicore) = 1
nextstateA(bicore) = 0
countB(bicore) = baselevel - inputaccB(bicore)
if bicore = 4 then // if motor bicore
motordiffR = diffvalue
motordiffL = 0
end if
end if
next bicore
state(all) = nextstate(all)
// update input accumulators
for bicore = 1 to 5
if bicore <> 5 then // not the photo bicore
for input = 1 to 2
source = sourceA(bicore, input)
weight = weightA(bicore, input)
if sourcestate(source) = on then
inputaccA(bicore) = inputaccA(bicore) + weight
if inputaccA(bicore) > maxinput then
inputaccA(bicore) = maxinput
end if
else
inputaccA(bicore) = inputaccA(bicore) - weight
if inputaccA(bicore) < 0 then
inputaccA(bicore) = 0
end if
end if
source = sourceB(bicore, input)
weight = weightB(bicore, input)
if sourcestate(source) = on then
inputaccB(bicore) = inputaccB(bicore) + weight
if inputaccB(bicore) > maxinput then
inputaccB(bicore) = maxinput
end if
else
inputaccB(bicore) = inputaccB(bicore) - weight
if inputaccB(bicore) < 0 then
inputaccB(bicore) = 0
end if
end if
next input
else // if photobicore
inputaccA(bicore) = left light level
inputaccB(bicore) = right light level
end if
next bicore
// drive motors
action = all 0
if motordiffL > 0 then
set leftforward bit in action
motordiffL = motordiffL - 1
end if
if motordiffR > 0 then
set rightforward bit in action
motordiffR = motordiffR - 1
end if
if leftfeeler touching and not leftignore then
set reverseright bit in action
end if
if rightfeeler touching and not rightignore then
set reverseleft bit in action
end if
if left motor reverse bit set then
set reverseleft bit in action
end if
if right motor reverse bit set then
set reverseright bit in action
end if
check for smoke and fix
apply action to motors
next microcycle
turn off motors
delay for a brief time
next sensecycle
else // power is low so...
sleep for a few seconds
end if
end loop forever
I practically had to rewrite the program in my mind to express structurally, as the machine code is anything but structured so the above doesn't exactly represent the program but is mostly equivalent. Not everything is specified, some of the lines represent entire subroutines like read senses. I tried to generalise it as much as possible for easy translation to other platforms, I don't really have 2-dimensional arrays but same idea.
With only 1K of program store available and few coding tools that support structured programming, the real program is written as unstructured spagetti-code. This is normal for PIC programming, users of larger processors with real compilers have it easy in this respect, but it is the price one has to pay to make use of a single chip computer that runs on 3 volts and a milliamp. To solarise and miniaturise a semi-intelligent autonomous agent one has to throw accuracy, intricacy and structure to the wind and work with the technology available. Or be stuck with batteries and a low survival score. Besides, the really good principles remain true even when simplified, so I am not complaining. Simple hardware forces simple solutions.
One advantage of simple processors, spagetti or not is there is only so much there, making program verification relatively easy. There are only so many ways it can go, and only the simulation engine needs to be bug free. I don't think very many people even understand the concept being simulated, I don't but that is why I am simulating it. It may remain a mystery but even if it does I still have an autonomous robot that has personality and can solve problems others in its class cannot.
Assembled Object Code
The following hex code represents the instructions for the PIC for running on the PicBot II Miniature robot platform. To replicate, copy the code between the cut lines into a .hex file then use PIC programming software to load into the processor. This hex dump was taken August 16 1999, program dated 8-16-99 12:12am.
-------------------------- cut -------------------------- :100000008F30620083120B101F306500C130660014 :1000100085018601831D13288C011830C4001E3011 :10002000A8001E30A9000618172863000028033016 :10003000BB0500303B020319362803303B0203198D :1000400036283A0895000430C100150894000330A2 :1000500094050030150203193628033015020319E0 :100060003628950C950CC10B25283A280130BB0089 :100070005530BA000F30C3000A308F003C234823AC :100080000C1C4C280C1949288C1949280430A8024A :1000900057280A30A80257280C1D51280130A807FC :1000A00057288C1D56280430A8078A1BA80A120856 :1000B000940013089407F8309405140845020318B7 :1000C00063280230A8074508140203186928023083 :1000D000A8021408C5004B302802031C71284B30BD :1000E000A800A81BA8010C187D280C197D288C19C4 :1000F0007D28A7172717A7122712A81BA82A44088C :100100002802031CD02A4B3028020319752A192310 :1001100005301402031CD02AE7302807031C92285C :100120001830C4003230C2003B08960000303F0255 :1001300003199D28BB18BF03A32816149610783006 :10014000BF001208BF02003040020319AA283B1862 :10015000C003B028961416107830C0001308C002EF :100160001608BB003A08BC00C101323084004108C7 :10017000840700089400003014020319E2280030BC :100180004102031DC728BA1C8C13BA188C17013002 :100190004102031DCF28BA1D8C13BA198C170230E7 :1001A0004102031DD728BA1E8C13BA1A8C170330CC :1001B0004102031DDF28BA1F8C13BA1B8C178C1B3E :1001C00094030C2900304102031DE8283C14BC10A4 :1001D00001304102031DEE283C15BC1102304102E2 :1001E000031DF4283C16BC1203304102031DFA28FB :1001F0003C17BC132A30840041088407000895008E :10020000373094001508940203304102031D0C2975 :100210002D231508BD00BE0132308400410884073B :1002200014088000363084004108840700089400D8 :100230000030140203193F2900304102031D242914 :100240003A1C8C133A188C1701304102031D2C29DB :100250003A1D8C133A198C1702304102031D3429C0 :100260003A1E8C133A1A8C1703304102031D3C29A5 :100270003A1F8C133A1B8C178C1B9403692900308E :100280004102031D4529BC143C1001304102031DED :100290004B29BC153C1102304102031D5129BC16EB :1002A0003C1203304102031D5729BC173C132E306A :1002B0008400410884070008950037309400150831 :1002C000940203304102031D69292D231508BE0045 :1002D000BD01363084004108840714088000C10A3B :1002E00004304102031CB5283C08BA00C101173094 :1002F000840041088407000894000F3094051922F7 :100300001F30840041088407000894000F309405D2 :100310002A30840041088407000895008C1F992921 :1003200014089507CD301507031C9D293230950020 :100330009D2914089502951B95012A3084004108D7 :100340008407150880001B308400410884070008DA :100350009400940E0F309405192223308400410834 :100360008407000894002E308400410884070008A8 :100370009500940E0F3094058C1FC729140895071B :10038000CD301507031CCB2932309500CB2914083A :100390009502951B95012E308400410884071508AD :1003A0008000C10A04304102031C77298E0100300D :1003B0003D020319DD29BD038E1500303E020319ED :1003C000E329BE038E168C13A71FEA290D1CEA2908 :1003D0000E168C17271FF0298D1CF0290E158C176F :1003E000A71EF4290E158C17271EF8290E168C1738 :1003F0008C1F042AA71D042A3A1B8E113A1F8E1542 :10040000BA1B8E12BA1F8E160E1D0A2A8E1D0A2ABC :100410000E118E110E1E102A8E1E102A0E128E1212 :100420000E0886006400C20B94288601C30B3C288A :10043000382B8C1301301402031D202A0D188C1741 :1004400002301402031D262A8D188C170330140263 :10045000031D2C2A0D198C1704301402031D322A97 :100460008D198C1705301402031D382A3B188C1780 :1004700006301402031D3E2ABB188C1707301402E5 :10048000031D442A0C188C1708301402031D4A2A35 :100490003A188C1709301402031D502ABA188C1709 :1004A0000A301402031D562A3A198C170B30140215 :1004B000031D5C2ABA198C170C301402031D622A22 :1004C0003A1A8C170D301402031D682ABA1A8C17B9 :1004D0000E301402031D6E2A3A1B8C170F301402C3 :1004E000031D742ABA1B8C1708000C1F8C2891223C :1004F000C1011730840041088407000888009A234E :10050000890AC10A11304102031C792A0C13A90A75 :10051000B4302907031C8C284B30A9001E30A800DA :100520008C2848230108960006309605890106307C :1005300016020319912A02301602031DA12A143053 :10054000890004301602031DA72A283089000800FC :100550009122C101962317308400410884070808BE :100560008000890AC10A11304102031CAA2A0C1317 :100570001E30A8001830C4000A30A902A91F8C2818 :10058000C101192317308400410884071408800032 :10059000C10A11304102031CC12A1E30A9008C2857 :1005A0000C172808C40048230108C1001E30C105EB :1005B0000310C10C19231730840041088407000878 :1005C0009500811EE82AF03094050F309505EC2A3D :1005D000F03095050F309405150894041730840009 :1005E0004108840714088000192314089500151C7D :1005F000022B951C022B192307309405F830A70510 :100600001408A704151D0D2B951D0D2B192338302B :100610009405C730A7051408A704151E8C28951E3D :100620008C281923C03094053F30A7051408A7046F :100630008C284823010896001E3096050310960C5E :100640004823010894001E309405940D940D940DD8 :10065000F030940516089404080027089500073028 :1006600095050310950D0310950D1E309507080094 :1006700064308F003C2313280F0890003C30910019 :10068000000000006400910B402B900B3E2B0800F3 :100690008D0185190D10851D0D1405188D10051C73 :1006A0008D141B30650085010A308F003C231F30FC :1006B00065007F3092000519612B00000000920B4D :1006C0005B2B1D30650085010A308F003C231F30F5 :1006D00065007F3093008518712B00000000930B9C :1006E0006B2B7E3092057E30930512081302031C9B :1006F0000D1513081202031C8D1513081202031D99 :10070000872BCD301207031C872B0D158D150C1D63 :100710008C110C198C150C1C0C110C180C150C14CC :100720000D18952B8D18952B0C10080083160814A6 :10073000831208003F30890583160815553089005B :10074000AA30890088148818A32B88128312080005 :100750000000000000000000000028346334293449 :1007600043346F34703472342E3431343934393484 :100770003934203462347934203457342E345434AC :10078000653472347234793420344E3465347734BD :1007900074346F346E34000000000000000000006C :1007A0000000000000000000000000000000000049 :1007B0000000000000000000000000000000000039 :1007C0000000000000000000000000000000000029 :1007D0000000000000000000000000000000000019 :1007E0000000000000000000000000000000000009 :1007F00000000000000000000000000000000000F9 :084000007F007F007F007F00BC :02400E00F73F7A :104200003000850086000C006E003000C600B30050 :104210003800F000AA00E000D4000A00F0004300DB :104220008C000000000000005000840089000C0099 :10423000600030000600B3003800F000AA00000063 :1042400054000A00F000B300C100000000000000AC :104250006000040089000C0060000000060083007C :104260005800A000AA00000054000A00B000B300EB :1042700087000000000000000000000000000000B7 :00000001FF -------------------------- cut --------------------------
The eeprom data block in the above translates into the following bicore array:
Memory slot # 1 Bicore in 1-A: LightOnLeft(3) + Always off(8) Bicore in 1-B: Photo-core out B(13) + Bicore out 4-A(4) Bicore in 2-A: Bicore out 1-A(15) + Photo-core out A(0) Bicore in 2-B: LightOnLeft(0) + Always off(10) Bicore in 3-A: Bicore out 1-A(10) + Photo-core out B(10) Bicore in 3-B: Bicore out 3-A(15) + Photo-core out B(0) Bicore in 4-A: Always off(14) + Bicore out 3-A(0) Bicore in 4-B: Bicore out 2-B(4) + LightOnLeft(3) Motorcon: IgnRightFeel NoDiffsInRev DiffNum = 4 Memory slot # 2 Bicore in 1-A: Photo-core out A(3) + Always off(8) Bicore in 1-B: Photo-core out B(5) + Always off(4) Bicore in 2-A: Bicore out 1-A(15) + LightOnRight(0) Bicore in 2-B: LightOnLeft(0) + Always off(10) Bicore in 3-A: Bicore out 1-A(10) + Bicore out 1-B(10) Bicore in 3-B: Always off(15) + Photo-core out B(0) Bicore in 4-A: Always off(0) + Bicore out 3-A(0) Bicore in 4-B: Bicore out 2-B(11) + LightOnLeft(3) Motorcon: DiffNum = 1 Memory slot # 3 Bicore in 1-A: Photo-core out B(5) + Always off(8) Bicore in 1-B: Photo-core out B(5) + Always off(4) Bicore in 2-A: Always off(10) + LightOnRight(0) Bicore in 2-B: Always off(0) + Always off(10) Bicore in 3-A: Bicore out 1-A(10) + Bicore out 1-B(10) Bicore in 3-B: Always off(11) + Photo-core out B(0) Bicore in 4-A: Always off(0) + Bicore out 3-A(0) Bicore in 4-B: Bicore out 1-A(11) + LightOnLeft(3) Motorcon: IgnRightFeel DiffNum = 7
Numbers in parenthesis are weights, 0 is the same as no connection. A and B correspond with left and right for photo-core (bicore 5 in the psuedocode), bicore 4-A feeds left motor, 4-B feeds right. Actual motor differentiator value is equal to DiffNum times 4 plus the minimum allowed value. With the minimum set at 30, 0-7 ranges diffvalue from 30 to 58. NoDiffsInReverse is a bit that when set does what it says, not represented in the pseudocode.
Technical eeprom data details:
0 |source1|source2| bicore 1 node A ---.
1 |source1|source2| bicore 1 node B |
. . . |
7 |source1|source2| bicore 4 node B | Slot 1
8 |weight1|weight2| bicore 1 node A |
. . . |
15 |weight1|weight2| bicore 4 node B |
16 |7|6|5|4|3|diff#| motorcon (*) ---'
20-36 Slot 2, as above
40-56 Slot 3, as above
(*) motorcon bits...
7/6 L/R 1=normal 0=ignorefeeler (resets to 1 when clear)
5/4 L/R 0=normal 1=reversemotor (resets to 0 when clear)
3 disconnect diff in reverse, drive with inverted bc out
0-2 DiffNum value
Input source coding:
0 Always read as 0
1/2 L/R feelers
3/4 light on left/right
5/6 photo-core A/B
7 badenv (feelerL or feelerR)
8-15 bicore 1-A out to bicore 4-B out
Discussion
The network in the code sample has connected itself mostly as a photovore; left light is applied to the right motor, right light is (indirectly) applied to the left motor. However if the light is blocked by an obstacle then strongly photovoric wiring schemes will score poorly once they get there, forcing development of alternate plans that spend about as much time going away from the light as towards, avoiding punishment and taking the one point reward it gets for not hitting anything. When it comes to self-organising systems the programmer is not in control, only makes suggestions. Often the programmer's plans are shoved aside in favor of plans that better satisfy the robot...
Memory slot # 1 Bicore in 1-A: Bicore out 3-B(2) + Bicore out 3-B(6) Bicore in 1-B: Bicore out 4-B(1) + LightOnLeft(11) Bicore in 2-A: Left feeler(4) + Bicore out 4-B(1) Bicore in 2-B: Always off(6) + Bicore out 2-A(10) Bicore in 3-A: Bicore out 3-A(9) + BadEnv flag(15) Bicore in 3-B: LightOnRight(3) + Photo-core out B(8) Bicore in 4-A: Always off(6) + LightOnLeft(13) Bicore in 4-B: LightOnRight(6) + Bicore out 3-A(10) Motorcon: ReverseRight DiffNum = 4 Memory slot # 2 Bicore in 1-A: LightOnRight(2) + Bicore out 3-B(14) Bicore in 1-B: Bicore out 1-B(7) + LightOnLeft(11) Bicore in 2-A: Always off(4) + Photo-core out A(13) Bicore in 2-B: Always off(6) + Bicore out 2-A(7) Bicore in 3-A: Bicore out 3-A(9) + BadEnv flag(15) Bicore in 3-B: Bicore out 1-B(6) + Photo-core out B(4) Bicore in 4-A: Bicore out 1-B(5) + LightOnLeft(13) Bicore in 4-B: Photo-core out A(6) + Bicore out 3-B(1) Motorcon: NoDiffsInRev DiffNum = 7 Memory slot # 3 Bicore in 1-A: LightOnRight(2) + Bicore out 3-B(6) Bicore in 1-B: Bicore out 4-B(7) + LightOnLeft(11) Bicore in 2-A: Always off(4) + Photo-core out A(13) Bicore in 2-B: Always off(6) + Bicore out 2-A(10) Bicore in 3-A: Bicore out 3-A(9) + BadEnv flag(15) Bicore in 3-B: LightOnRight(3) + Photo-core out B(4) Bicore in 4-A: Always off(14) + LightOnLeft(13) Bicore in 4-B: Left feeler(6) + LightOnRight(10) Motorcon: DiffNum = 3
It seems to have turned into a light-avoiding robot.
The ReverseLeft/Right and IgnLeft/RightFeel flags are not supposed to show up in saved copies, supposed to be cleared after three good moves. Must be a bug or a misunderstanding. Newer versions of the program are coded to reset those flags so I won't have to see them, but behaviorally they seem no better or worse. I can't say that my scoring function is particularly effective, the simpler method of simply punishing for feeler contact and rewarding otherwise works too. Observably the effects are very subtle and difficult to qualify without considerable study. The underlying horse layer in this particular creation is very adept at solving basic navigational problems all by itself, generally it will randomly select the reverse action to back away in about 8 moves then it should stick (unless it learns to do it otherwise). The code is programmed to clear the flags so it will use the feelers and not be backing up (another last minute hack - thought it would be nice to have self-control over reverse actions) but for some strange reason networks still get saved with the bits enabled. I think I'm beginning to understand why... (maybe not but trying to think positively:) reverse actions are not seen at all by the scoring function so are perfectly acceptable, they will clear themselves if there is no need, and with the new scoring function there is a reward for successful obstacle avoidance - careful, it might very well learn to seek out obstacles just to avoid them, but not making contact enough to negatively impact the score, this can be done by twiddling the ignore and reverse bits. Then it saves. This part of it has nothing to do with bicores, but having an adaptable layer underneath the bicores frees them to do what they do best - generate semi-chaotic patterns in response to input stimuli, leading to the production of path-tracing oscillations that guide it around obstacles. If you don't reward too much for hitting them. The programmer can suggest, but often the environment-robot system will interpret the cues in unexpected ways. The programmer is not really in control, having only the power to "mess it up", but not necessarily make it work as expected.
I grew tired of messing it up, so I went back to the hex code I used in this document for another overnight run, this time in a smaller tray devoid of obstacles besides the walls. The light was positioned so that it was beyond the edge of the tray. Here's what it produced:
Memory slot # 1 Bicore in 1-A: Bicore out 4-B(3) + Photo-core out A(3) Bicore in 1-B: Right feeler(11) + Photo-core out A(9) Bicore in 2-A: Bicore out 4-A(6) + Bicore out 2-B(2) Bicore in 2-B: Left feeler(7) + Photo-core out A(1) Bicore in 3-A: Always off(5) + Bicore out 1-B(2) Bicore in 3-B: Photo-core out B(1) + Bicore out 3-A(5) Bicore in 4-A: Bicore out 2-B(7) + Bicore out 3-A(10) Bicore in 4-B: Photo-core out B(9) + LightOnRight(15) Motorcon: DiffNum = 7 Memory slot # 2 Bicore in 1-A: Bicore out 4-B(3) + Photo-core out A(3) Bicore in 1-B: Right feeler(11) + Photo-core out A(9) Bicore in 2-A: Bicore out 4-A(6) + Bicore out 2-B(2) Bicore in 2-B: Left feeler(7) + Photo-core out A(1) Bicore in 3-A: Always off(5) + Bicore out 1-B(2) Bicore in 3-B: Photo-core out B(1) + Bicore out 3-A(5) Bicore in 4-A: Bicore out 2-B(7) + Bicore out 4-B(10) Bicore in 4-B: Photo-core out B(9) + LightOnRight(15) Motorcon: DiffNum = 1 Memory slot # 3 Bicore in 1-A: Bicore out 4-B(3) + Photo-core out A(3) Bicore in 1-B: Right feeler(5) + Photo-core out A(11) Bicore in 2-A: Bicore out 4-A(6) + Bicore out 1-A(2) Bicore in 2-B: Bicore out 1-A(7) + Photo-core out A(1) Bicore in 3-A: Always off(5) + Bicore out 1-A(3) Bicore in 3-B: Photo-core out B(1) + Bicore out 3-A(5) Bicore in 4-A: LightOnRight(14) + Bicore out 4-B(10) Bicore in 4-B: Left feeler(9) + LightOnRight(15) Motorcon: NoDiffsInRev DiffNum = 4
At least it didn't save with those pesky horse flags enabled. It appears to have completely transformed from the starting state, aparently wiring up light-avoiding connections as in the previous run but it is hard to state without running the network to see what kind of output it produces. At least there is a bit more diversity, still not what I'd like to see but not surprising given the limited population size. Lesson: just because a term is present in the scoring function does not mean the robot will do what it implies, particularly if the term conflicts with other terms. Because the robot cannot get to the light, the term cannot be satisfied without scoring poorly because of excessive feeler contact.
Tenative Conclusions
It acts like it is alive. It fights if you mess with it, or tries to run. If something is in its way and it can't get around, it will try to push the object out of the way. Neat, but this is simply a side-effect of being able to select different speeds and being able to temporarily ignore its feelers.
This needs more research before hard conclusions can be reached, but tentively I conclude:
"Living Machines" by Brosl Hasslacher and Mark W. Tilden:
http://www.geocities.com/SouthBeach/6897/living_machines.pdf
(found on Chiu-Yuan Fang's beam web site:
http://www.geocities.com/SouthBeach/6897/beam2.html)
Mark Tilden's Nervous Network Patent:
http://www.xs4all.nl/~vsim/amiller/patent.html
(found on A.A. van Zoelen's robotic page:
http://www.xs4all.nl/~vsim/robotics.html
in his mirror of Andrew Miller's walker page)
Brian Bush's BEAM faq:
http://people.ne.mediaone.net/bushbo/beam/main.html
"Biomorphic Robots and Nervous Net Research: A New Machine Control Paradigm" by Mark W. Tilden: http://people.ne.mediaone.net/bushbo/beam/Biomorphic.html (from Brian Bush's page)
The PicBot II robot design, by Terry Newton:
http://www.nc5.infi.net/~wtnewton/otherwld/robot5.html
Mirror of David Tait's page for obtaining SPP programming software, look for "16F84 in-circuit programmers": http://www.dontronics.com/dtlinks.html
Just a (very) small sampling of evolved/genetic neural network papers...
"Incremental Evolution of Neural Network Architectures for Adaptive Behavior" by D.Cliff, I.Harvey, P.Husbands, CSRP256, December 1992 University of Sussex
"An Evolutionary Algorithm that Constructs Recurrent Neural Networks" by P.Angeline, G.Saunders, J.Pollack, Laboratory for Artificial Intelligence Research, Ohio State University
"Embodied Evolution: Embodying an Evolutionary Algorithm in a Population of Robots" by R.Watson, S.Ficici, J.Pollack, Dynamical and Evolutionary Machine Organization, Volen Center for Complex Systems, Brandeis University
Hundreds of papers partially about this stuff are available at Cora Research
Paper Search:
http://cora.jprc.com/Artificial_Intelligence/Machine_Learning/Genetic_Algorithms/index.html
How much of it is correct I cannot say, but there's a lot of it. Don't let
your head explode!
This document was last modified August 16, 1999, minor editing March 25,
2000
Contents (C) Copyright 1999, 2000 by Terry Newton
email: wtnewton@nc5.infi.net
End of Document